Clinical data are inherently hierarchical and relational, yet most machine learning models embed electronic health records in Euclidean latent spaces that erase this structure. In generative settings, this misalignment causes transport dynamics to collapse hierarchy, degrading interpretability and robustness. My research studies how latent geometry and transport constraints can be explicitly modeled to preserve clinical structure while maintaining predictive accuracy.

A central premise of my work is that model behavior is governed as much by transport dynamics as by architecture or capacity. While prior work has explored geometry-aware representations, transport is often treated implicitly—optimized for likelihood or reconstruction accuracy without regard for how trajectories reshape latent manifolds. I instead treat transport as a first-class modeling object, asking when transport parameterization—rather than model expressivity—determines hierarchical fidelity. In earlier experiments with hyperbolic embeddings and rectified-flow transport, I observed that geometry-aware choices can improve predictive performance while producing unstable or hyperparameter-sensitive structural behavior. These observations motivated my core research question: when can hierarchy preservation and predictive accuracy coexist intrinsically, and when is structure maintained only through external constraints rather than the transport dynamics themselves?

To study geometry–transport interactions in a controlled manner, I developed a synthetic ICD trajectory benchmark based on rooted medical ontologies. This framework isolates structural fidelity from predictive accuracy, allowing systematic evaluation across Euclidean and hyperbolic generative regimes. Experiments revealed a consistent pattern: Euclidean models achieved reasonable accuracy while collapsing hierarchy, whereas unconstrained hyperbolic models preserved structure but became unstable as depth increased. These results indicated that geometry alone is insufficient—transport must be explicitly constrained for structure preservation to be stable rather than incidental.

These insights informed HyperMedDiff-Risk, a geometry-aware diffusion framework for clinical risk prediction. The model integrates hyperbolic ICD embeddings aligned via hyperbolic diffusion distance, graph diffusion encoders that propagate relational structure, and rectified-flow transport designed to prevent hierarchical collapse during generation. Unlike prior diffusion-based clinical models operating in Euclidean latent spaces, HyperMedDiff-Risk explicitly couples geometry and transport throughout training.

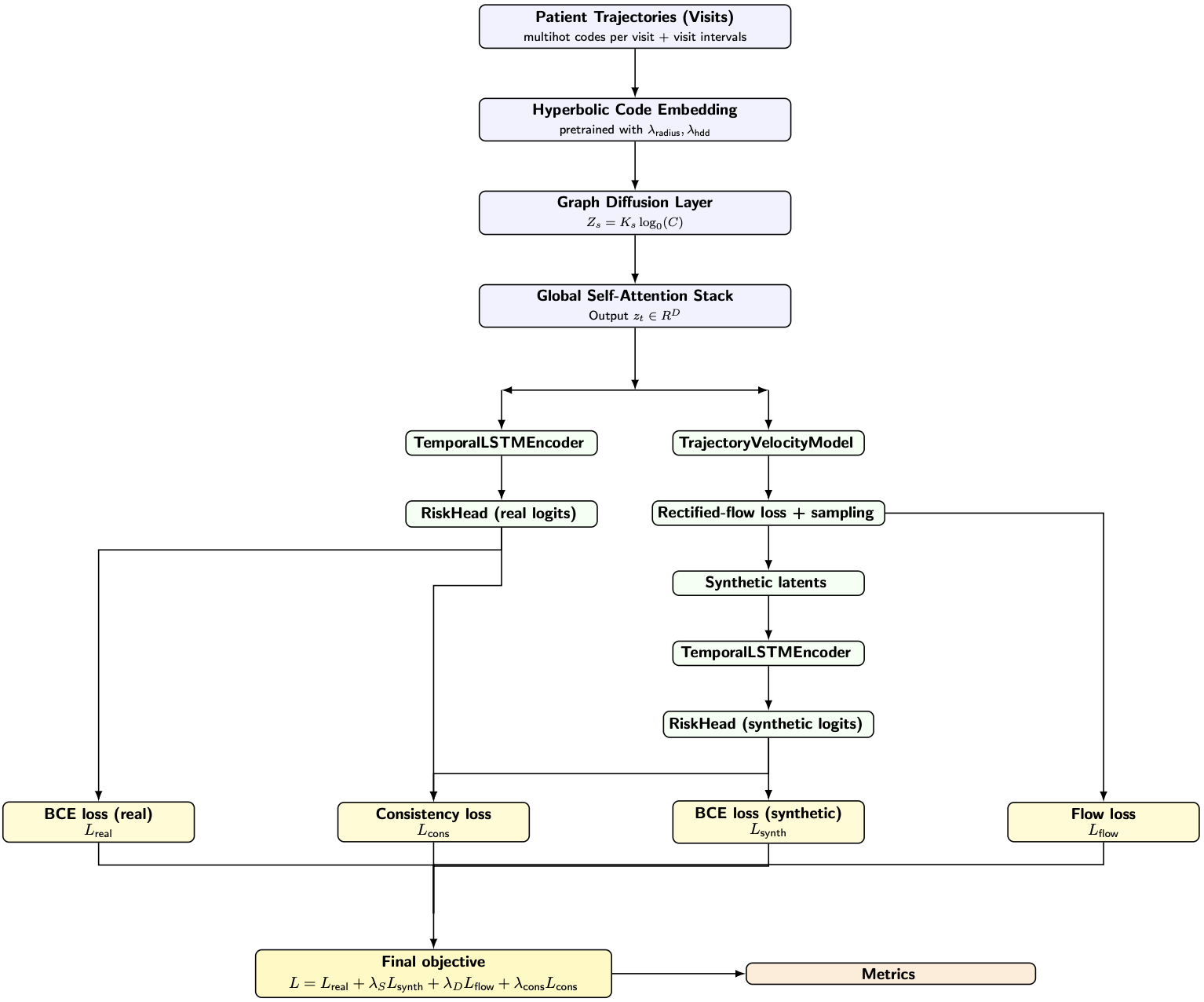
On the MIMIC-III heart-failure cohort, HyperMedDiff-Risk outperforms MedDiffusion, achieving higher AUPRC and Cohen’s κ while maintaining improved hierarchical fidelity. Ablation studies quantify how curvature, diffusion depth, decoder expressivity, and regularization strength trade off structural preservation and predictive accuracy, highlighting regimes in which hierarchy is preserved robustly versus those in which it is sustained only through external constraints. A manuscript detailing these findings is currently in preparation.

My ongoing work extends this framework by studying transport-constrained diffusion and flow models on curved manifolds, with an emphasis on identifying stability regimes under increasing depth and noise. This includes fully hyperbolic pipelines where rectified flows operate via parallel-transported velocities, sequence models remain on-manifold through the risk loss, and curvature-adaptive step size controls maintain stability. I am exploring multi-scale geometric representations that jointly encode ontological hierarchy, temporal dynamics, and graph structure, as well as geometry-driven interpretability methods that keep explanations faithful to clinical organization rather than post-hoc approximations.

While my current focus is EHR-based risk prediction, these questions naturally generalize to multimodal biomedical data, including imaging, genomics, and ontology-grounded foundation models. My long-term objective is to develop transport-aware geometric learning frameworks that bridge theory and deployment in biomedical AI, enabling models whose theoretical behavior and empirical performance are jointly characterized. Through this work, I aim to contribute foundational insights into geometry-aware generative modeling while advancing systems that translate reliably to real clinical impact.